Daß sich der Pfeil beim Abschuß vom Bogen erheblich durchbiegt, ja daß dieses Durchbiegen erst ein genaues Schießen mit dem System Pfeil und Bogen möglich macht, ist bekannt. Jeder etwas engagierte Bogenschütze/schützin wird dafür sorgen, daß sein System Bogen/Pfeil stimmt.
Zur Abstimmung steht eine fast unendliche Anzahl von
Was davon notwendig und nützlich ist, steht auf einem anderen Blatt. Als Hilfe in diesem Dschungel dienen Pfeilauswahltabellen und Rechnerprogramme, die im Wesentlichen von Easton bestimmt werden.
Feinabstimmungsmethoden zur Optimierung des Pfeilfluges sind zur Genüge bekannt, wirken aber leider erst, wenn die Pfeile gekauft sind. Sie haben weiter den Nachteil, daß nur Spitzenschützen damit umgehen können, weil nie auf die Streuung eingegangen wird und die Lage eines einzelnen Schusses zur Bewertung herangezogen wird. Bevor aber weiter diskutiert wird, sollte der Begriff "Optimierung" definiert werden:
Unter Optimierung wird hier der Prozeß verstanden, an dessen Ende der Pfeil ausgewählt ist, der
Zuerst soll die Auswahlmethode nach Easton betrachtet werden. Die angeblich in die Betrachtung eingehenden Größen sind entweder unwichtig (z.B. Federngröße und Anzahl, Tillerabstand) oder reichen nicht aus, um den Bogen, oder genauer sein Verhalten beim Schuß genügend genau zu beschreiben.
Nach dieser Methode wird ein Pfeil gefunden, der zum Fliegen (der unbefiederte Pfeil wird sich nach mühseliger Suche nach dem passenden Spitzengewicht in der Gruppe der Befiederten wiederfinden) gebracht wird, von einer Optimierung kann aber nicht geredet werden.
Außerdem hat das Programm Fehler. So reagiert ein Pfeil mit einer leichteren Spitze mit Sicherheit in Richtung "steifer" und nicht "weicher", wie ein vorliegender Rechnerausdruck ausweist.
Das Eastonprogramm ist mehr oder weniger eine Ansammlung von Daten, die den bekannten Tabellen und Diagrammen entspricht und durch Zu- und Abschläge den Eindruck einer exakten Berechnung erweckt.
Welche Größen müssen vorliegen, um auf Anhieb den passenden Pfeil und die dazugehörende Spitzen/Schaftmassenkombination zu finden?
Mehr ist nicht notwendig, um die Durchbiegung des Pfeiles als Funktion der Zeit zu beschreiben.
Alle weiteren Angaben (Sehnenart, Strangzahl, Sehnenstandshöhe, Tiller, usw usf ) beinhalten entweder obige Angaben verklausuliert oder sind einfach unbrauchbar.
Mit der hier beschriebenen Methode wird die primäre elastische Durchbiegung des Pfeiles während des Schußvorganges durch die auf ihn einwirkenden Beschleunigungskräfte beschrieben. Die weiteren Biegeschwingungen ergeben sich aus der
Unter Steife ist hier die technische Steife gemeint, die sich als Produkt des Elastizitätsmoduls mit dem Flächenträgheitsmoment des Pfeilquerschnittes darstellt. Diese Steife ist bei Pfeilen leicht aus dem Spinewert errechenbar.
f(weg) ⇒ (-0.3810 + 3.4191*weg - 11.3468*weg2 +21.6742*weg3 - 24.27371*weg4 + 15.5488*weg5 - 4.41785*weg6)
Das ist in diesem Fall ein Polymon 6.Ordnung und beschreibt die Auszugskurve eines bestimmten Bogens. Diese Kurve muss experimentell einwandfrei mit relativ hoher Genauigkeit bestimmt werden. Aus dieser Kurve wird mit entsprechendem Programm ein Polynom erstellt.
Diese Funktion wird um die Ordinate gespiegelt. Mit der Pfeilmasse und der virtuellen Masse, die sich aus Anteilen der dynamischen Wurfarmmasse und der Sehnenmasse zusammensetzt, ergibt sich die Beschleunigungskurve des Pfeiles als Funktion des Weges:
a(weg) ⇒ (46597.7912*(-0.2812 + 1.6840*(0.709 - weg) - 0.6892*(0.709-weg)2-9.6436*(0.709-weg)3 +24.0010*(0.709-weg)4-22.0759*(0.709-weg)5 +7.2683*(0.709 - weg)6))
Das Diagramm zeigt die Beschleunigung des Pfeiles über den Weg. Der Start ist jetzt natürlich durch das Lösen der Sehne des gespannten Bogens gegeben. Man erkennt, daß die Spitzenbeschleunigung beachtliche 700g beträgt, und das bereits bei einer Endhaltekraft des Bogens von ca 160N.
Diese Gleichung wird zu einer Differentialgleichung zweiten Grades umgeschrieben:
s''[t]==[46597.7912*(-0.2812 + 1.6840*(0.709 -s[t]) -0.6892*(0.709 - s[t])2 - 9.6436*(0.709 - s[t])3 + 24.0100*(0.709-s[t])4-22.0759*(0.709-s[t])5 + +7.2683*(0.709 - s[t])6), {s[0]==0, s'[0]==0.},s[t],{t,0,0.015}].
Die Randbedingungen sind dadurch gegeben, daß zu Startbeginn der Weg und die Geschwindigkeit gleich 0 sind. Weiterhin muß dem Rechner gesagt werden, daß die numerische Lösung in der Zeit t zwischen 0 und 15ms durchzuführen ist. Das Ganze ist natürlich ein Feder-Masse System, wovon allerdings nur ein kleiner Zeitabschnitt betrachtet wird, da sich ja am Ende der Schußzeit der Pfeil von der Sehne löst und damit der Ansatz nicht mehr gültig ist.
Diese Gleichung ist nicht analytisch lösbar, sondern nur numerisch. Als Ergebnis bekommt man die Beschleunigung des Pfeiles als Funktion der Zeit und hat damit die Grundlage zur Berechnung der Durchbiegung des Pfeiles als Funktion der Zeit.
Hier die Darstellung der Funktion. Es ist zu sehen, daß der Schußvorgang nach 12ms abgeschlossen ist. Bei etwas über 12ms verläßt in diesem Fall der Pfeil die Sehne.
Zur Berechnung der Durchbiegung wird die Eulersche Knickgleichung angewendet. Hierbei ist die kritische Knickkraft bzw die kritische Knicklänge eine wichtige Größe. Unterhalb dieser Grenzen tut sich garnichts, der Pfeil biegt sich nicht. Aus der kritischen Knickkraft läßt sich die Zeitspanne errechnen, in der die primäre Durchbiegung durch die auftretende Beschleunigung auftritt, aus der kritischen Knicklänge bei der maximalen Beschleunigung der Massenanteil des Pfeiles abschätzen, der mit der Spitzenmasse und der Beschleunigung die zeitlich abhängige Knickkraft ergibt.
Nach 3ms ist die Beschleunigung soweit abgesunken, daß der Pfeil nicht mehr durchgebogen werden kann. Der Pfeil hat bis dahin einen Weg von 0.034m zurückgelegt. Nach dieser Strecke führt der Pfeil nur noch nach den durch Steife, Länge und Masse vorgegebenen Bedingungen Biegeschwingungen aus.
Für den behandelten Fall hat der Pfeil eine Eigenfrequenz von 44 Hz, Der Schwingungsknoten, dort wo man anfassen sollte, wenn man den Pfeil zum Schwingen bringt, um evtl beschädigte Pfeile auszusortieren, liegt 16cm unterhalb des Nocks.
Wie sehen die praktischen Ergebnisse der beschriebenen Optimierungsrechnung aus?
Für Bögen mit Endhaltekräften von 115N bis 190N und Pfeillängen von 0.6m bis 0.8m wurden Pfeilkodes in den Pfeilsorten ACE, ACC, Navigator, ACG, Beman und Aluminium durchgerechnet. In den Fällen in denen die Überprüfung durch Beschuß stattfand, konnte immer eine 100%ige Abstimmung festgestellt werden. An zwei Beispielen soll es hier dokumentiert werden.
Für einen guten Schützen wurde ein ACE Pfeil optimiert. Das heißt, er gab einen mit seinem Schießstil sehr gut fliegenden und von ihm gut überprüften Pfeil an. Dieser Pfeil bildete die Referenz. Der optimierte Pfeil hatte folgende Eigenschaften:
Hier das Treffbild der befiederten Pfeile auf 50m.
Dieses Treffbild wurde vor jeder weiteren Untersuchung aus reiner Neugier geschossen:
Das Treffbild wurde ohne Verstellung der Pfeilanlage, nach nur wenigen Probeschüssen, mit welchen die Höheneinstellung des Visieres eingeschossen wurde, erstellt. Die grünen Kreuze bezeichnen Schüsse, die der Schütze selber als nicht optimal (Abschußfehler) erkannt hat. Ein weiterer Kommentar erübrigt sich. Das folgende Bild zeigt den Abstimmungstest auf 18m:
Auch hier wurde keine Veränderung an der Pfeilanlage vorgenommen. Eine Veränderung des Nockpunktes auf der Sehne ist ebenfalls noch nicht erfolgt. Die Auswertung erfolgte mit dem Auswerteprogramm Schießsportergebnisse A.Sch.E. von Markus Nentwig
Das nächste Beispiel beschreibt die Optimierung eines Hallenpfeiles. Hier kommt es weniger auf eine gestreckte Flugbahn und damit eine Minimierung von Umwelteinflüssen an, sondern es sollte der Aluminiumpfeil X7 1914 (es heißt ja, mit dicken Pfeilen gibt es mehr Ringe, obwohl schon vor Jahren im Bogensportmagazin "The Glade" der Beweis geführt wurde, daß diese Annahme nur für Weltklasseschützen zutrifft, ab Ringzahlen von 590 aufwärts können es 2 bis 3 Ringe sein) zum Fliegen gebracht werden.
Die erste Analyse ergab, daß er viel zu steif war. Dies zeigte sich sogar an Schleifspuren am Pfeil. Die Spitze wurde um 0.0015 kg schwerer gemacht (jawohl, kein Schreibfehler), das Ergebnis zeigen die folgenden Bilder. Auch hier erfolgte keinerlei Veränderung der Pfeilanlage und des Nockpunktes auf der Sehne.
Ein Test auf eine Schußentfernung von 9m zeigte übrigens, daß der Nockpunkt stimmte. Der Höhenunterschied bei 18m erklärt sich aus den verwendeten Naturfedern.
Mit der Pfeilanlage ist übrigens kein wesentlicher Einfluß auf die Abstimmung des Pfeiles erreichbar.
Erreichbar ist eine Verlagerung des Treffbildes und vielleicht, eine Auswirkung auf die Streuung. Auf keinen Fall kann mit Federspannung und Vorstand der Pfeilanlage ein nicht passender Pfeil zum vernünftigen Flug gebracht werden. Dazu ist die Kontaktzeit zu kurz und sind die einwirkenden Kräfte zu groß.
Mit den beiden Beispielen konnte gezeigt werden, daß es analytische Methoden gibt, den passenden Pfeil zu bestimmen und sich viel Probieren und Frust zu ersparen. Diese Untersuchung kann nicht von jedermann durchgeführt werden und ist, da trotz Rechner der Zeitaufwand relativ hoch ist, nicht für einen Appel und ein Ei zu haben.
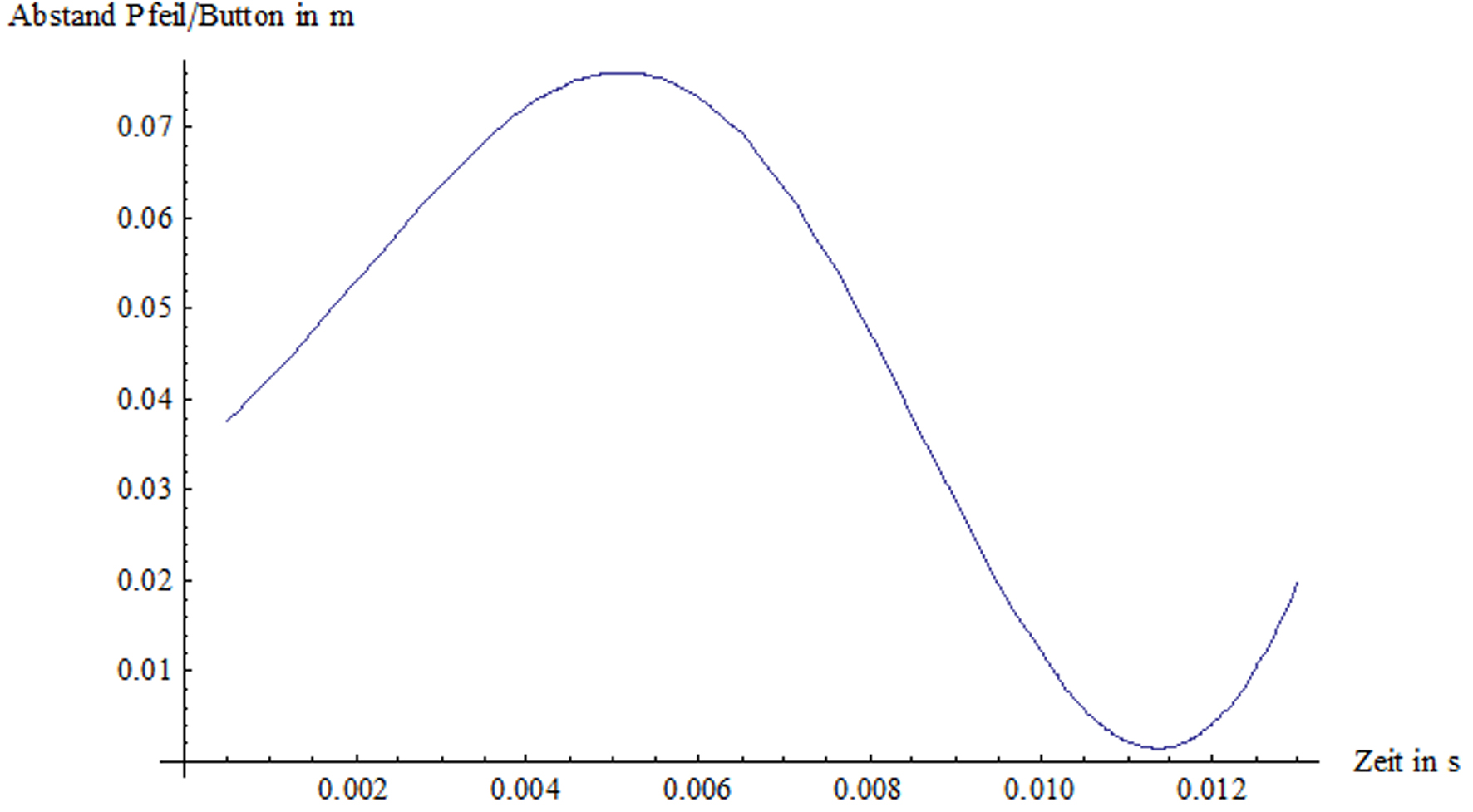
Abstand Pfeilschaft-Button während des Schusses
Geändert am 17. Sep. 2022
Geändert am 25. Aug 2007Literatur:
Dubbel, 17. Auflage
Pfeilflug wie auf Schienen, Gabriel
http://home.rhein-zeitung.de/cnentwig (Technik)
Hier habe ich einen Beitrag in einem Forum für Bogenschießen gefunden, in dem wirklich anschaulich der Vorgang der Pfeilschwingung
im Bogen beschrieben wird.
Er wird mit ausdrücklicher Erlaubnis des Autors b_der_k_te hier veröffentlicht:
Und hier der dazugehörige Screenshot, der in der pdf Datei nicht aufgeht
Dieser Screenshot stammt nach Angaben
des Autors aus Berechnungen von James L. Park. Dieser rechnet die Pfeilbewegung wissenschaftlich genau. Meine Modellrechnung ist für
praktische Zwecke gedacht, mit ihr können die ersten zwei bis drei Millisekunden nicht beschrieben werden,
und sie berücksichtigt nur die erste Grundschwingung. Aber sie schneidet auch im Vergleich mit der wissenschaftlichen Herangehensweise
nicht schlecht ab. Jedenfalls reicht sie aus, die Abstimmung sehr exakt und in allen bisher durchgeführten Berechnungen zutreffend zu beschreiben.