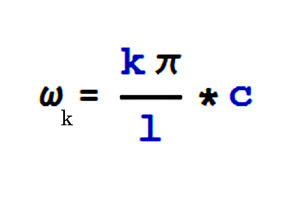Zugkraft (Zugspannung) in der Sehne

Da hat ein User in einem Forum einen wirklich kreativen Gedanken hineingebracht, wie zumindest qualitativ im Versuch nachgewiesen werden kann ob die Zugspannung und damit natürlich die Zugkraft in der Sehne beim Spannen des Bogens steigt oder fällt.

1. Mein Ansatz in meinen Modellen ist, das die Zugkraft/Spannung beim Spannen konstant bleibt

2. In "Archers Technology" von Dr. James Park, Seite 20 statisch) und Seite 26 (dynamisch) bleibt die Zugkraft über einen weiten Bereich mehr oder weniger gleich, erst gegen Ende der Schußzeit ( gesamt ca 12-14ms) steigt sie, -bei sehr kleinen dynamischen Wurfarmmassen sogar dramatisch- an. In keinem Fall, weder statisch (Spannen) noch dynamisch (während der Schußzeit) steigt sie mit zunehmendem Auszug.

3. Auf den ersten Blick (und das sieht ja von außen betrachtet auch ziemlich logisch aus), sollte die Zugkraft mit zunehmendem Auszug steigen. Das ist ein klarer Fehlschluss, wenn man physikalisch/technisch analysiert. Dieser Fehlschluss wird ausgenutzt, um dem Sehnengarn irgendwelche Eigenschaften anzudichten, die das eine oder andere Garn besser geeignet zum Bogenschießen hinstellen sollen.

Diese drei Denkansätze gibt es, und der User hat einen Versuch beschrieben, den jeder nachvollziehen kann, um das qualitativ zu überprüfen. Ich zitiere:
Also was tun für eine schnelle, qualitative Antwort? Nun, einfach eine Sehne auf einen Bogen gespannt, Mittelteil mit dem Fuß auf dem Teppich fixieren, mit der einen Hand (besser einem Finger) die Sehne nach oben kontinuierlich ausziehen und mit der anderen Hand an der Sehne fortwährend zupfen. Ergebnis: Der Ton wird mit zunehmendem Auszug deutlich hörbar ... tiefer. Also nimmt die Spannung ab (auch dann wenn die Sehne nicht mehr am Wurfarmende aufliegt).

Ja, fast genial. Kompliment.

Beim Spannen ändert die Sehne ihre Schwingungslänge. Sein Ansatz wäre vollkommen richtig bei nem klassischen Langbogen. Beim Recurve stimmt das nicht. Die Eigenfrequenz einer Sehne/Saite ist:

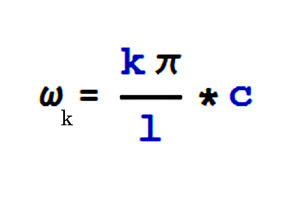
"k" ist Freiheitsgrad (1...2...3... ) bei k=1 wird der tiefste Ton erzeugt,
F [N] ist die Spannkraft,
μ ist die spezifische Masse der Saite pro Meter
μ=m_sehne/l [kg/m]]
c²=F/μ
"l" die Länge der Saite in Meter.
Nimmt man die Spannkraft als konstant an, die spez. Masse der Sehne sowieso, ist die Eigenfrequenz nur noch von ihrer Länge abhängig. Die ist bei einem Recurve nicht konstant, sondern ändert sich mit der Länge des Auszuges, bis die gesamte Sehne vollständig frei wird.
Je länger die Sehne, umso tiefer der Ton...
Und anders herum, bleibt die Sehnenlänge konstant und wird der Ton tiefer, dann muß sich die Spannkraft ändern. Sie muß kleiner werden.

Quelle: Dubbel, Taschenbuch für den Maschinenbau

1. Test

Aufbau:
Einer spannte den Bogen, eine (Krickeline war die Harfinistin) zupfte die Saite/Sehne, und ein Musiker der Rheinischen Philharmonie horchte... Das Ergebnis war hochinteressant:
Der leichte Bogen (wettkampfmäßige Ausrüstung, Endhaltekraft ca 22lbs bei Auszugslänge 73cm):
Der Ton blieb gleich.
Der Wettkampfbogen (30lbs bei 73cm Auszugslänge):
Der Ton wurde tatsächlich tiefer... Beim Start ist das keine Überraschung, die Saite/Sehne wird ja länger. Aber auch, als die Sehne nur noch Kontakt über die Pressung am Wurfarmende hatte, wurde der Ton bei längerem Auszug prinzipiell tiefer. Jedenfalls scheint es so, als wäre der Verlauf der Spannkraft während des Ausziehens auch von der Stärke des Bogens und von der Auszugscharakteristik abhängig.

2. Test

Ja, und dann bekam ich eine nette e-mail eines Instrumentenbauers, ich zitiere in voller Länge:
Hallo Christian
Als Instrumentenbauer hat mich das Thema mit der Sehnenspannung nicht los gelassen und so habe ich gerade mal selbst den Versuch gemacht, vielleicht interessant für Dich:
Und zwar mit einem Langbogen, die Sehne ist also zu jedem Zeitpunkt frei.
Bogen: Earl Hoyt jr. "Sky Trophy", 69", 60#, Also ein modernes, glasbelegtes Möbelstück
Sehne: Dakron, von der Stange, ich glaube 16 Strang.
Ich war zunächst etwas verwirrt, denn direkt nach dem Aufspannen wollte sich kein so rechtes Bild abzeichnen, was die Tonhöhe bei ansteigender Auszugslänge anging. Es schien zunächst einfach höher zu werden... Dann sich kaum zu ändern... Nach etwa 5 min auf dem Bogen und mehrmaligem Ausziehen ergab sich jedoch das erwartete Schema: Es wurde beim Ausziehen eindeutig tiefer. Nicht um sehr viel, aber für mich deutlich hörbar. Ausserdem fiel mir auf, dass das Absinken der Stimmung nicht ganz linear zu sein scheint, wie es die Berechnungen ja auch nahe legen. Das bleibt aber ein subjektiver Eindruck. Fuss drauf, mit einer Hand ziehen und mit der Anderen zupfen ist ja nun kein gültiger Laborversuch.
Ich werde dennoch mal versuchen, ob mein Stimmgerät in der Lage ist, da einen Ton zu erfassen, leider ist es ja mehr ein Geräusch, also ein diffuser Frequenzsalat, damit kommen auch teurere Stimmgeräte meist nicht gut klar. Nach Gehör würde ich sagen, zwischen Ruhestellung und Vollauszug liegen etwa 20ct.
Akustische Grüße,
Arno

Diskussion

Abschließend der kluge Post eines Fachmannes. Er ist auch dahingehend wichtig, weil er sehr gut beschreibt, wie die hineingespeicherte Energie auf die Sehne wirkt, wenn sich die Sehnenkraft beim Ausziehen doch deutlich verringert: Zitat:
... Die Wurfarme werden beim Auszug tatsächlich stärker gebogen weil die Sehne kürzer wird. (Beim Dacron am Beispiel oben wären das 3mm pro WA-Seite.) Die Energie dazu kommt aus der Sehne selbst. Sie wurde eingebracht als der Bogen aufgespannt wurde. Entsprechend kurz muß die Sehne sein um überhaupt auf die gewünschte Standhöhe zu kommen. Es kommt beim Ausziehen also nicht per se mehr Energie in den gesamten Bogen. Der Schütze braucht laut berechneter Auszugskurve sogar weniger Energie von außen über die aufgebrachte Auszugskraft (mal Auszugslänge) zuführen. Zu dem Zusammenspiel von Auszugslänge, Sehnenwinkel und WA-Biegung um zur Auszugskurve zu gelangen, kommt halt noch die variable Sehnenlänge hinzu.

Was für Auswirkungen hat das? Ich nehme mal das Beispiel des Posters
F_{1 Sehne Standhöhe}= 402N
F_{2 Sehne Endauszug}= 261N
Verkürzung der Sehne beim Spannen (Dacron) Δs= 5mm

Dann wäre die Energie, die die Sehne ab bzw wieder aufnimmt:
W_Sehne=(F₁-F₂)/2*Δs
W=0.35Nm. Das ist mehr oder weniger die Formänderungsarbeit durch elastische Verformungen. Wie groß ist dieser Einfluss? In Summa: kein Einfluss. Hickman hatte schon recht, wenn er zur Vereinfachung die Sehne als unendlich starr annahm. Und ich auch, weil ich andersrum die Sehnenkraft als konstant ansetze... Sonst würden mein Abstimmungen nicht so gut passen.
Zur Illustration: die Masse der Sehne geht zu einem Drittel in die virtuelle Masse ein. Das bedeutet, bei einem 20g schweren Pfeil, der eine kinetische Energie von 36Nm (entsprechend 60m/s) hat, wären das bei einer Sehnenmasse von 6g ca 3,6Nm.Die elastische Dehnung, egal ob bei Dacron oder FF oder irgendwelchen anderen Garnen spielt keine Rolle.

Das einzige, was physikalisch beim Sehnengarn eine Rolle spielt, ist die Masse. Vergleicht man Sehnen gleicher Masse, aber mit unterschiedlichen Garnen untereinander (Und ja, nicht nur UHMW Polyethylen, da ist Dacron und auch Aramid prinzipiell mit eingeschlossen), wird man weder bei der Abstimmung Pfeil-Bogen noch bei der Außenballistik einen Unterschied feststellen.

Zurück zur Website